If Two Variables Are Highly Correlated
Multicollinearity in Regression
Why it is a problem? How to bank check and fix it

Multicollinearity happens when independent variables in the regression model are highly correlated to each other. It makes it hard to interpret of model and as well creates an overfitting problem. It is a mutual assumption that people examination before selecting the variables into the regression model.
I encountered a serious multicollinearity event before when I built the regression model for time series data. I created multiple features based on unlike time periods like one-month total render, 6-month total render, and 1-year full return to have more input variables. However, these features are highly correlated with each other. For example, if i stock has performed well for the by year, then it is very probable to have done well for the recent calendar month. I would need to either drib some of these variables or find a mode to make them less correlated. I will explain subsequently in the article different ways to solve the problem.
Why Multi-Collinearity is a trouble?
When independent variables are highly correlated, change in i variable would crusade change to some other and then the model results fluctuate significantly. The model results will be unstable and vary a lot given a small alter in the data or model. This volition create the following issues:
- It would be hard for yous to choose the list of significant variables for the model if the model gives yous different results every time.
- Coefficient Estimates would not be stable and it would be hard for yous to translate the model. In other words, you cannot tell the scale of changes to the output if ane of your predicting factors changes past 1 unit.
- The unstable nature of the model may crusade overfitting. If yous employ the model to another sample of data, the accuracy will driblet significantly compared to the accuracy of your training dataset.
Depending on the situation, it may not exist a trouble for your model if only slight or moderate collinearity outcome occurs. However, information technology is strongly brash to solve the issue if severe collinearity outcome exists(e.grand. correlation >0.8 between 2 variables or Variance inflation factor(VIF) >20 )
How to check whether Multi-Collinearity occurs?
The first simple method is to plot the correlation matrix of all the independent variables.
I used the housing data from the Kaggle competition. The goal of the competition is to utilize the housing information input to correctly predict the sales toll. I have selected a few numerical variables to be included in my model here.
#plot color scaled correlation matrix
corr=house_selected.corr()
corr.style.background_gradient(cmap='coolwarm') 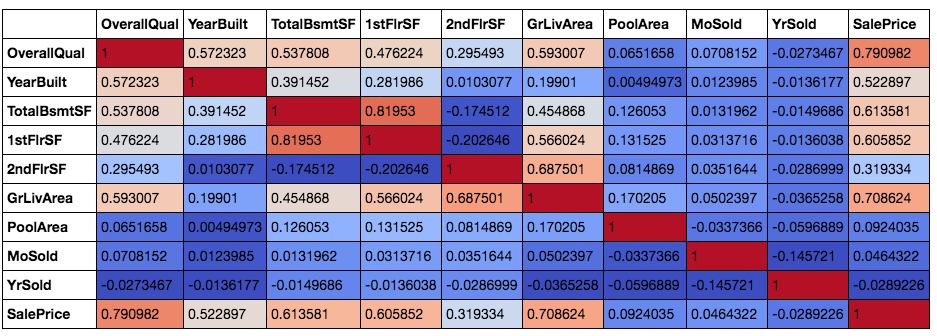
Afterwards plotting the correlation matrix and color scaling the groundwork, we can see the pairwise correlation between all the variables. I accept included the dependent variable 'SalePrice' hither equally well. This is because it is a secret trick for me when I try to select the contained variables to be included in the model.
When y'all are clueless about which variables to include in the model, just practice a correlation matrix and select those independent variables with loftier correlation with dependent variable.
Back to the Multi-Collinearity result, we can see that from the correlation matrix, quite a few variables are correlated to each other. There is ane pair of independent variables with more than than 0.8 correlation which are full basement surface area and first-floor surface area. Houses with larger basement areas tend to take bigger first-flooring areas as well and and so a high correlation should exist expected.
The second method to check multi-collinearity is to use the Variance Inflation Factor(VIF) for each independent variable. Information technology is a measure of multicollinearity in the prepare of multiple regression variables. The higher the value of VIF the higher correlation betwixt this variable and the rest.
#Compute VIF data for each independent variable
from statsmodels.stats.outliers_influence import variance_inflation_factor
vif = pd.DataFrame()
vif["features"] = house_selected.columns
vif["vif_Factor"] = [variance_inflation_factor(house_selected.values, i) for i in range(house_selected.shape[i])]
vif 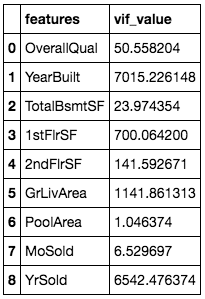
If the VIF value is higher than 10, it is usually considered to have a loftier correlation with other independent variables. However, the acceptance range is subject to requirements and constraints. From the results, we can come across that most features are highly correlated with other independent variables and only two features tin pass the below ten threshold.
How to fix the Multi-Collinearity event?
- Variable Choice
The most straightforward method is to remove some variables that are highly correlated to others and leave the more meaning ones in the fix. For example, when we plot the correlation matrix with 'SalePrice' included, we tin see that Overall Quality and Ground living area have the two highest correlations with the dependent variable 'SalePrice' and thus I will try to include them in the model.
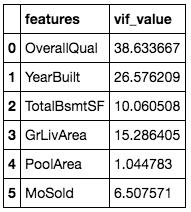
We tin meet that using simple elimination, we are able to reduce the VIF value significantly while keeping the of import variables. However, some of the variables like Overall Quality and Years of Built still have high VIF value and they are important in predicting housing price. How? Sometimes nosotros can use minor tricks equally described in the second method later to transform the variable.
2. Variable Transformation
The second method is to transform some of the variables to make them less correlated but still maintain their feature. What practise I mean past this? In the housing model example, I can transfer 'years of built' to 'age of the firm' by subtracting current yr by years of built. For example, if the year of building is1994, then the age of the house is 2020–1994=26 years.
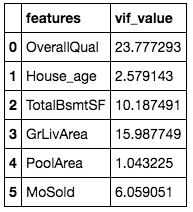
After I catechumen the years of building to house age, the VIF for the new 'House_age' factor drops to an acceptable range and the VIF value for overall quality also drops.
In the example of fourth dimension serial analysis which I mentioned at the offset, I besides converted variables to make them less correlated. For example, the full return for the past one month is highly correlated with the past six months' total render. I subtracted the past i-month render from the by 6-month render to become the new variable on the previous five-month render which does not include the past calendar month. The correlation results are much more acceptable and I was able to include both variables equally my model features.
3. Principal Component Analysis
Principal Component Analysis(PCA) is ordinarily used to reduce the dimension of data by decomposing information into a number of independent factors. It has many applications like simplifying model calculation by reducing the number of predicting factors. However, in our case here, we will just use the character of variable independence for PCA to remove the multi-collinearity outcome in the model.
#Create the new data frame by transforming data using PCA
import numpy equally np
from sklearn.decomposition import PCA
pca = PCA(n_components=6)
components=pca.fit_transform(house_adjusted)
componentsDf=pd.DataFrame(data=components,columns=['component 1','component ii','component iii','component 4','component five','component 6']) #Calculate VIF for each variable in the new information frame
vif = pd.DataFrame()
vif["features"] = componentsDf.columns
vif["vif_value"] = [variance_inflation_factor(componentsDf.values, i) for i in range(componentsDf.shape[i])]
vif
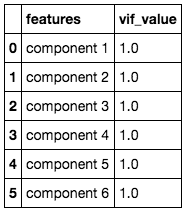
I still keep the same number of variables compared to the original data and we tin run into that now the vi variables are non correlated to each other at all. Nosotros tin use the new 6 variables as the contained variables to predict housing prices.
The drawback of this method is as well very obvious. After PCA transformation, we do not have the identity for each variable and it volition be hard to interpret the results.
Determination & Recommendation
We should check the outcome of Multi-Collinearity every time before we build the regression model. VIF would be an piece of cake way to await at each contained variable to see whether they accept a high correlation with the rest. A correlation matrix would be useful to select of import factors when you are not certain which variables to select for the model. The correlation matrix also helps to understand why sure variables have high VIF values.
In terms of methods to prepare the multi-collinearity issue, I personally do non prefer PCA hither because model interpretation volition be lost and when you want to apply the model to another prepare of data you demand to PCA transform again. Thus, we should endeavour our best to reduce the correlation by selecting the right variables and transform them if needed. Information technology is your telephone call to decide whether to keep the variable or not when information technology has a relatively high VIF value merely also important in predicting the issue. Trial and fault is always the instance to include dissimilar sets of variables, build the model and test information technology against testing information to run across whether at that place is any overfitting.
Do yous think you are finally done with all the checks with statistical assumptions before constructing a model? No, yous are not! If y'all desire to know more most other statistical assumptions in a regression model, refer to my other article beneath on Normality Assumption in the regression model.
Source: https://towardsdatascience.com/multi-collinearity-in-regression-fe7a2c1467ea
0 Response to "If Two Variables Are Highly Correlated"
Post a Comment